UP Mathematician Develops Model For Heat Propagation Through Rough Surfaces
By: Harvey Sapigao
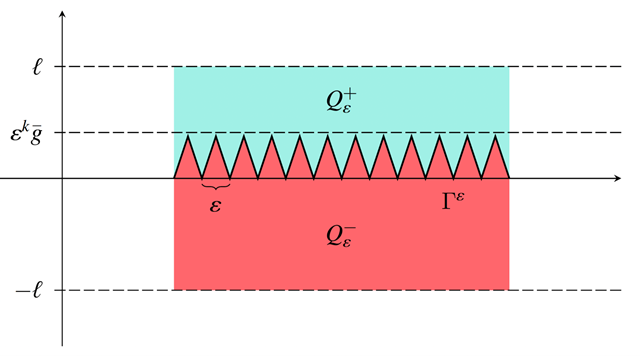
Model for two materials with a rough interface (Photo Credit: Avila et. al. 2024)
Suppose you have a pair of pants you need to wear tomorrow. The problem is, you just washed them, and they’re still damp. So you resort to a handy tool: the flat iron.
Using the iron, you can easily dry the flat parts of the pants, but you will notice that it is more difficult to dry some areas where the surface is uneven – near the zipper, the side and back pockets, the seams, and the waistband.
That’s because the heat from the iron does not reach the uneven areas as quickly as it does the flatter areas. In other words, the heat propagation, or the heat transfer from the iron to the pants, is not uniform on rough surfaces.
Understanding how heat propagates from one material to another is important in designing efficient cooling devices, such as air conditioners, or constructing infrastructures that minimize heat from the sun. In some cases, heat propagation is simple to model when the boundary at which the two materials touch is flat, such as ironing the flat areas of the pants. In other cases, however, the heat propagation model is more complex when the boundary is rough, such as when ironing the uneven areas of the pants.
Jake Avila of the UPD College of Science Institute of Mathematics (UPD-CS IM) formulated a theory to model heat propagation through rough surfaces. With the help of mathematicians in Italy, Avila’s theory uses a method called homogenization.
Homogenization is a way of combining the tiny details of the material with its bigger, more uniform properties. For example, the flat areas of the pants may look flat under the naked eye, but if you examine them under a microscope, you will notice the individual bumps made by the interwoven threads, which don’t look flat at all. “Homogenization theory aims to describe the macroscopic or effective properties of composite materials while taking into account simultaneously the microscopic or local properties of its components,” explained Avila.
Homogenization helps simplify the problem and provides a more accurate model for heat propagation. According to Avila, homogenization incorporates the effective properties of the material, such as the thermal conductivity, while also considering the individual features of the material’s components.
Although he only applied his theory to heat propagation, it can be used for other physical phenomena as well. “[It] can also be applied to describe the acoustic wave propagation over rough walls or the turbulence flow in the rough ocean surface,” Avila said.
The next step is to develop a more general version of the theory for wider application. “The next plan is to study a more complicated and general problem wherein a sign-changing density function is involved in the eigenvalue problem in a domain through rough surfaces,” said Avila. “The problem in the article is a special case where a unit density function is treated.” (PR)







